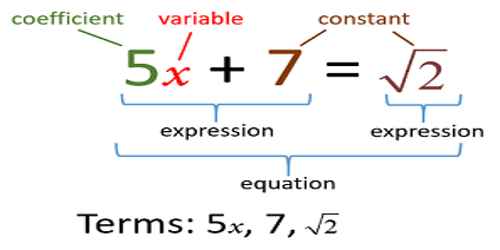Variable and Constant
Constants and Variables are the two types of symbols in algebra. In Mathematics, we usually deal with two types of quantities-Variable quantities (or variables) and Constant quantities (or constants). If the value of a quantity remains unaltered under different situations, it is called a constant. On the contrary, if the value of a quantity changes under different situations, it is called a variable. A Variable is a symbol for a number we don’t know yet. It is usually a letter like x or y. A number on its own is called a Constant.
For example: 4, 2.718, 22/7 etc. are constants while speed of a train, demand of a commodity, population of a town etc. are variables.
Constant
A symbol which has a fixed numerical value is called a constant.
For example: 2, 5, 0, -3, -7, 2/7, 7/9 etc., are constants.
Number of days in a week represents a constant.
In the expression 5x + 7, the constant term is 7.
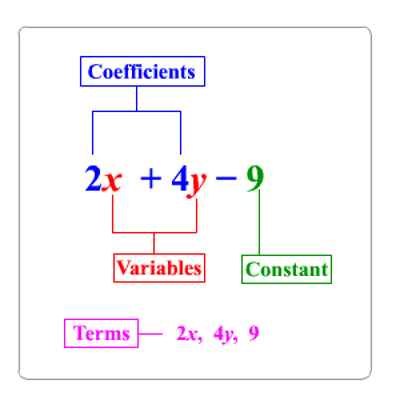
Variables
A quantity which has no fixed value but takes no various numerical values is called a variable.
For example:
Temperature at different times of a day represents a variable.
The height of a student in your grade is a variable, as it varies from student to student. A variable is denoted by a letter like x, y, z, u, v etc.
A combination of a constant and a variable is also a variable. Variables are use to hold the value or store some result and the value of variables can be changed but we cannot assign some value to a constant. Constant have their fix value which cannot be changed.
Difference between Variables and Constants
- Variables are quantities with changing magnitude, hence can assume different values based on the application.
- Constants are quantities with unchanging values, and used to represent numbers with significance.
- Both constants and variables are represented algebraically by English or Greek letters.
- Constants are used to represent quantities in nature which are fixed, and the variables are used to represent unknowns.
In problems relating to two or more variables, it is seen that the value of a variable changes with the change in the value (or values) of the related variable (or variables). Suppose a train running at a uniform speed of v km./h. travels a distance of d km. in t hours. Obviously, if t remains unchanged then v increases or decreases according as d increases or decreases. But if d remains unchanged, then v decreases or increases according as t increases or decreases. This shows that the change in the value of a variable may be accompanied differently with the change in the values of related variables. Such relationship with regards to the change in the value of a variable when the values of the related variables change, is termed as variation.
Information Source: