Mathematical induction is a technique for proving a statement – a theorem, or a formula — that is asserted about every natural number. It is a mathematical proof technique used to prove a given statement about any well-ordered set. Most commonly, it is used to establish statements for the set of all natural numbers.
1 + 2 + 3 + 4 + ..… + n = {n(n + 1)}/2.
For all positive integers n.
We denote this mathematical statement by P(n). If n = 1, then we find that {1(1 + 1)}/2= 1.
Hence the above statement is true for n = 1.
Suppose n = 2. Then 1 + 2 = 3 and {2(2 + 1)}/2= 3. So we find that the statement is true for n = 2.
Thus, it is easy to verify that P(n) is true for n = 1, 2, 3 or 4. But it is impossible to verify that the above statement is true for all positive integers.
To prove that the above statement P(n) is true for all positive integers we generally follow a method of proof which is known as proof by the Principle of Mathematical Induction or simply proof by mathematical induction. For this we assume the following important property of integers.
Principle of Mathematical Induction:
Let P(n) be a mathematical statement about nonnegative integers n and n be a fixed nonnegative integer.
(1) Suppose P(n₀) is true i.e.. P(n) is true for n = n₀.
(2) Whenever k is an integer such that k ≥ n₀ and P(k) is true, then
P(k + 1) is true.
Then P(n) is true for all integers n ≥ n₀.
The above property of integers is also called First Principle of Mathematical Induction. We now show how to prove.
1 + 2 + 3 + …………..+ n = {n(n + 1)}/2 ,
for all integers n ≥ 1 by mathematical induction.
Let P(n) be the statement
1 + 2 + 3 + …………..+ n = {n(n + 1)}/2, for all integers n ≥ 1
For n = 1, 1 = 1(1 + 1)/2 holds. Hence P(1) is true. Let k be an integer such that k ≥ 1. Assume that P(k) is true. Now
1 + 2 + 3 + ……. + k + (k + 1) = (1 + 2 + 3 + …….. + k) + (k + 1)
= {k(k + 1}/)2 + (k + 1) (since P(k) is true)
= (k + 1)(k/2 + 1)
= (k + 1){(k + 2)/2}
= {(k + 1)(k + 2)}/2.
Thus we find that P(k + 1) is true. Hence by mathematical induction it follows that P(n) is true for all integers n ≥ 1.
We note that a proof by mathematical induction consists of three steps.
- Step 1. (Basis) Show that P(n₀) is true.
- Step 2. (Inductive hypothesis). Write the inductive hypothesis: Let k be an integer such that k ≥ n₀ and P(k) be true.
- Step 3. (Inductive step). Show that P(k + 1) is true.
We have an equivalent statement of the Principle of mathematical induction which is often very useful. This equivalent statement is called strong form of mathematical induction or Second principle of mathematical induction.
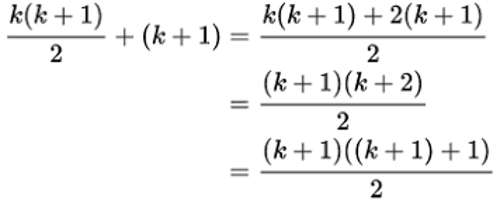
Second Principle of Mathematical Induction:
Let P(n) be a mathematical statement about nonnegative integers n and n₀ be a fixed nonnegative integer. Suppose P(n₀) is true. If for any integer k ≥ n₀ ‘P(n₀ + 1), P(n₀ + 2), …. ..,P(k) arc true implies that P(k + 1) is true’, then P(n) is true for all is n ≥ n₀.
Once can prove that the First Principle of Mathematical Induction holds if and only if the Second Principle of Mathematical Induction holds. For this proof one can see any standard book on algebra. Let us now show some application of this principle. For this we consider Fibonacci sequence f₁, f₂, f₃, ……. , where f₁ = 1 ,f₂ = 1, and f₀ = f₀ + f₀ for n ≥ 3.
Then
f₃ = f₁ + f₂ = I + 1 = 2,
f₄ = f₂ + f₃₀ = 1 + 2 = 3, and so on.
Information Source: