About Fluorescence
Definition
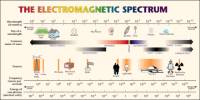
Fluorescence is a form of luminescence, which is the emission of light not attributed to thermal radiation, that occurs over very short time scales – around 10-9 – 10-7s. The first fluorescent substance to be observed and recorded was quinine sulphate a key ingredient in tonic water. The most striking example of fluorescence occurs when the absorbed radiation is in the ultraviolet region of the spectrum, and thus invisible to the human eye, while the emitted light is in the visible region, which gives the fluorescent substance a distinct color that can only be seen when exposed to UV light. Fluorescent materials cease to glow immediately when the radiation source stops, unlike phosphorescence, where it continues to emit light for some time after.

Using fluorescence to create an image in microscopy has been in use since the 1940’s, but there has been a greatly increased interest in using fluorescent molecules in microscopy since the advent of the laser scanning confocal microscope in the late 1980’s.
Fluorescence has many practical applications, including mineralogy, gemology, medicine, chemical sensors (fluorescence spectroscopy), fluorescent labelling, dyes, biological detectors, cosmic-ray detection, and, most commonly, fluorescent lamps. Fluorescence also occurs frequently in nature in some minerals and in various biological states in many branches of the animal kingdom.
Principles of Fluorescence
Fluorescence is based on the property of some molecules that when they are hit by a photon, they can absorb the energy of that photon to get into an excited state. Upon relaxation from that excited state, the same molecule releases a photon: fluorescence emission. The energy of the photon that is released is always lower than that of the photon that was absorbed. So the photon that excites the dye always has a smaller wavelength than the photon that gets emitted.
The fluorescence quantum yield gives the efficiency of the fluorescence process. It is defined as the ratio of the number of photons emitted to the number of photons absorbed. The maximum fluorescence quantum yield is 1.0 (100%); each photon absorbed results in a photon emitted. Compounds with quantum yields of 0.10 are still considered quite fluorescent. Fluorescence quantum yields are measured by comparison to a standard. The quinine salt quinine sulfate in a sulfuric acid solution is a common fluorescence standard.
Strongly fluorescent pigments often have an unusual appearance which is often described colloquially as a “neon color.” This phenomenon was termed “Farbenglut” by Hermann von Helmholtz and “fluorence” by Ralph M. Evans. It is generally thought to be related to the high brightness of the color relative to what it would be as a component of white. Fluorescence shifts energy in the incident illumination from shorter wavelengths to longer and thus can make the fluorescent color appear brighter (more saturated) than it could possibly be by reflection alone.
Fluorescence in Nature
Fluorescence is generated when a material absorbs high-energy photons and then emits photons of lower energy. The Optical Microscopy Division of the National High Magnetic Field Laboratory at Florida State University explains that when a fluorescent material absorbs a photon, the excess energy is lost as heat that is subsequently absorbed by neighboring molecules in the material. As a result, photons are re-emitted at lower energies that are now within the range visible to the human eye, making the material appear to glow. Therefore, in order for fluorescent materials to fluoresce, they normally need to be exposed to higher energy light, such as ultraviolet light.

Biofluorescence is the absorption of electromagnetic wavelengths from the visible light spectrum by fluorescent proteins in a living organism, and the reemission of that light at a lower energy level. This causes the light that is re-emitted to be a different color than the light that is absorbed. Stimulating light excites an electron, raising energy to an unstable level. This instability is unfavorable, so the energized electron is returned to a stable state almost as immediately as it becomes unstable. This return to stability corresponds with the release of excess energy in the form of fluorescent light. This emission of light is only observable when the stimulant light is still providing light to the organism/object and is typically yellow, pink, orange, red, green, or purple. Biofluorescence is often confused with the following forms of biotic light, bioluminescence and biophosphorescence.
Pigment cells that exhibit fluorescence are called fluorescent chromatophores, and function somatically similar to regular chromatophores. These cells are dendritic, and contain pigments called fluorosomes. These pigments contain fluorescent proteins which are activated by K+ (potassium) ions, and it is their movement, aggregation, and dispersion within the fluorescent chromatophore that cause directed fluorescence patterning.

Use Fluorescence for Monitoring Water Quality
A significant proportion of chromophoric (light absorbing/coloured) organic matter is fluorescent when excited by light in the UV region. Distinct fluorescent peaks have been identified and related to certain ‘types’ of organic matter. For example, humic-like or CDOM fluorescence can be traced back to terrestrial production by vascular plants. Microbial or protein – like fluorescence is largely related to in-stream production by algae and bacteria. These peaks show strong relationships with conventional water quality parameters such as Total Organic Carbon and Biochemical Oxygen Demand.