Pauli Exclusion Principle
Definition
The Pauli Exclusion Principle states no two electrons or other fermions can have the identical quantum mechanical state in the same atom. In the case of electrons in atoms, it can be stated as follows: it is impossible for two electrons of a poly-electron atom to have the same values of the four quantum numbers: n, the principal quantum number, ℓ, the angular momentum quantum number, mℓ, the magnetic quantum number, and ms, the spin quantum number. For example, if two electrons reside in the same orbital, and if their n, ℓ, and mℓ values are the same, then their ms must be different, and thus the electrons must have opposite half-integer spins of 1/2 and −1/2. The principle was proposed by Austrian physicist Wolfgang Pauli in 1925 to describe the behavior of electrons. In 1940, he extended the principle to all fermions in the spin-statistics theorem.

In 1925, Wolfgang Pauli gave physics his exclusion principle as a way to explain the arrangement of electrons in an atom. His hypothesis was that only one electron can occupy a give quantum state. That is, each electron in an atom has a unique set of quantum numbers, the principle quantum number which gives its energy level, the magnetic quantum number which gives the direction of orbital angular momentum, and the spin quantum number which gives the direction of its spin. If this principle did not hold, all of the electrons in an atom would pile up in the lowest energy state.
Subatomic particles fall into two classes, based on their statistical behaviour. Those particles to which the Pauli Exclusion Principle applies are called fermions; those that do not obey this principle are called bosons. When in a closed system, such as an atom for electrons or a nucleus for protons and neutrons, fermions are distributed so that a given state is occupied by only one at a time.
Particles obeying the Pauli Exclusion Principle have a characteristic value of spin, or intrinsic angular momentum; their spin is always some odd whole-number multiple of one-half. In the modern view of atoms, the space surrounding the dense nucleus may be thought of as consisting of orbitals, or regions, each of which comprises only two distinct states. The Pauli Exclusion Principle indicates that, if one of these states is occupied by an electron of spin one-half, the other may be occupied only by an electron of opposite spin, or spin negative one-half. An orbital occupied by a pair of electrons of opposite spin is filled: no more electrons may enter it until one of the pair vacates the orbital. An alternative version of the exclusion principle as applied to atomic electrons states that no two electrons can have the same values of all four quantum numbers.
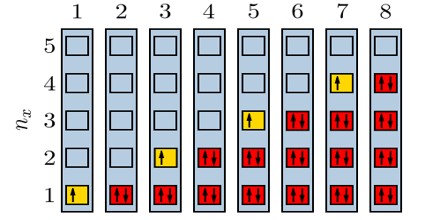
Pauli Exclusion Principle in Science
The principle that two fermions of a given type, such as electrons, protons, or neutrons, cannot occupy the same quantum state. It does not apply to bosons. This principle plays a key role in the electron orbital structure of atoms, since it prevents more than two electrons from occupying any given orbital, two are allowed, since they may have opposite spin, and thus be in different quantum states.
Pauli Exclusion Principle in Advanced Quantum Theory
The Pauli Exclusion Principle is an example of a quantum principle that states that no two particles can have the same quantum numbers.
In relativistic quantum field theory, the Pauli principle follows from applying a rotation operator in imaginary time to particles of half-integer spin.
In one dimension, bosons, as well as fermions, can obey the exclusion principle. A one-dimensional Bose gas with delta-function repulsive interactions of infinite strength is equivalent to a gas of free fermions. The reason for this is that, in one dimension, exchange of particles requires that they pass through each other; for infinitely strong repulsion this cannot happen. This model is described by a quantum nonlinear Schrödinger equation. In momentum space the exclusion principle is valid also for finite repulsion in a Bose gas with delta-function interactions, as well as for interacting spins and Hubbard model in one dimension, and for other models solvable by Bethe ansatz. The ground state in models solvable by Bethe ansatz is a Fermi sphere.
Consequences
One particularly important consequence of the principle is the elaborate electron shell structure of atoms and the way atoms share electrons, explaining the variety of chemical elements and their chemical combinations. An electrically neutral atom contains bound electrons equal in number to the protons in the nucleus. The stability of the electrons in an atom itself is unrelated to the exclusion principle, but is described by the quantum theory of the atom. The underlying idea is that close approach of an electron to the nucleus of the atom necessarily increases its kinetic energy, an application of the uncertainty principle of Heisenberg. However, stability of large systems with many electrons and many nucleons is a different matter, and requires the Pauli Exclusion Principle.
The consequence of the Pauli principle here is that electrons of the same spin are kept apart by a repulsive exchange interaction, which is a short-range effect, acting simultaneously with the long-range electrostatic or Coulombic force. This effect is partly responsible for the everyday observation in the macroscopic world that two solid objects cannot be in the same place at the same time.