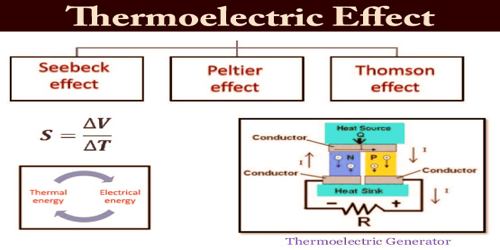
The thermoelectric effect is a phenomenon by which a temperature difference is directly converted to electric voltage and vice versa. When two dissimilar metals such as iron and copper are joined at both ends to form a closed circuit, and one of the junctions is at a higher temperature than the other, a current is set up. The e.m.f. driving this current is called a ‘thermoelectric e.m.f.’, and the phenomenon is known as the Thermoelectric effect or Seebeck effect after the German physicist ‘Thomas Johann Seebeck’ discovered it in 1821. This effect can be used to generate electricity, to measure temperature, to cool objects, or to heat them or cook them. Because the direction of heating and cooling is determined by the sign of the applied voltage, thermoelectric devices make very convenient temperature controllers.
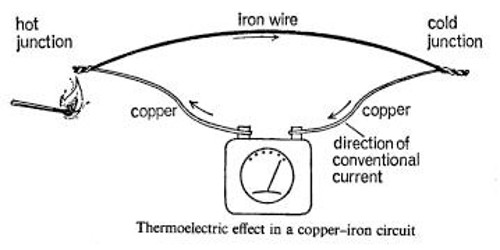
Usually a thermoelectric e.m.f. is very small, only a few millionths of a volt. For a copper-iron circuit it is found to be about 7lV for every degree Centigrade of temperature difference between the junctions; for antimony and bismuth it is as high as 100 lV per deg C, while for copper and Constantan (55 per cent copper, 45 per cent nickel), the two metals most often used in practice, it is 40 lV per deg C of temperature difference.
Traditionally, the term thermoelectric effect or thermoelectricity encompasses three separately identified phenomena, known as the Seebeck effect, the Peltier effect, and the Thomson effect. In many textbooks, thermoelectric effect may also be called the Peltier–Seebeck effect. This separation derives from the independent discoveries of French physicist Jean Charles Athanase Peltier and Estonian-German physicist Thomas Johann Seebeck. Joule heating, the heat that is generated whenever a voltage difference is applied across a resistive material, is somewhat related, though it is not generally termed a thermoelectric effect (and it is usually regarded as being a loss mechanism due to non-ideality in thermoelectric devices). The Peltier–Seebeck and Thomson effects are reversible, whereas Joule heating is not.
Seebeck Effect –
The Seebeck effect is the buildup of an electric potential across a temperature gradient. A thermocouple measures the difference in potential across a hot and cold end for two dissimilar materials. This potential difference is proportional to the temperature difference between the hot and cold ends. First discovered in 1794 by Italian scientist Alessandro Volta, it is named after the Baltic German physicist Thomas Johann Seebeck, who in 1821 independently rediscovered it. It was observed that a compass needle would be deflected by a closed loop formed by two different metals joined in two places, with an applied temperature difference between the joints. This was because the electron energy levels shifted differently in the different metals, creating a potential difference between the junctions which in turn created an electrical current through the wires, and therefore a magnetic field around the wires. Seebeck did not recognize that an electric current was involved, so he called the phenomenon “thermomagnetic effect”. Danish physicist Hans Christian Ørsted rectified the oversight and coined the term “thermoelectricity”.
The Seebeck effect is commonly used in a device called a thermocouple (because it is made from a coupling or junction of materials, usually metals) to measure a temperature difference directly or to measure an absolute temperature by setting one end to a known temperature. Several thermocouples when connected in series are called a thermopile, which is sometimes constructed in order to increase the output voltage since the voltage induced over each individual couple is small. This is also the principle at work behind thermal diodes and thermoelectric generators (such as radioisotope thermoelectric generators or RTGs) which are used for creating power from heat differentials.
Peltier Effect –
The Peltier effect bears the name of Jean-Charles Peltier (a French physicist) who discovered in 1834, the calorific effect of an electrical current at the junction of two different metals. When a current I is made to flow through the circuit, heat is evolved at the upper junction (at T2), and absorbed at the lower junction (at T1). The Peltier heat absorbed by the lower junction per unit time, Q is equal to
Q = ΠAB I = (ΠB – ΠA) I
Where Π is the Peltier coefficient ΠAB of the entire thermocouple, and ΠA and ΠB are the coefficients of each material. P-type silicon typically has a positive Peltier coefficient (though not above ~550 K), and n-type silicon is typically negative, as the names suggest.
The Peltier coefficients represent how much heat is carried per unit charge. Since charge current must be continuous across a junction, the associated heat flow will develop a discontinuity if ΠA and ΠB are different. The Peltier effect can be considered as the back-action counterpart to the Seebeck effect (analogous to the back-EMF in magnetic induction): if a simple thermoelectric circuit is closed, then the Seebeck effect will drive a current, which in turn (by the Peltier effect) will always transfer heat from the hot to the cold junction. The close relationship between Peltier and Seebeck effects can be seen in the direct connection between their coefficients: Π = TS
A Peltier cooler/heater or thermoelectric heat pump is a solid-state active heat pump which transfers heat from one side of the device to the other. Peltier cooling is also called thermo-electric cooling (TEC).
Thomson Effect –
The Thomson effect The Thomson effect was predicted and subsequently experimentally observed by William Thomson (Lord Kelvin) in 1851. It describes the heating or cooling of a current-carrying conductor with a temperature gradient. Any current-carrying conductor (except for a superconductor), with a temperature difference between two points, will either absorb or emit heat, depending on the material.
If a current density J is passed through a homogeneous conductor, the Thomson effect predicts a heat production rate per unit volume
q = KJ . ΔT,
where ΔT is the temperature gradient, and K is the Thomson coefficient. The Thomson coefficient is related to the Seebeck coefficient as K=TdS/sT. This equation, however, neglects Joule heating and ordinary thermal conductivity.
The Thomson coefficient is unique among the three main thermoelectric coefficients because it is the only thermoelectric coefficient directly measurable for individual materials. The Peltier and Seebeck coefficients can only be determined for pairs of materials. Thus, there is no direct experimental method to determine an absolute Seebeck coefficient (i.e. thermopower) or absolute Peltier coefficient for an individual material. However, as mentioned elsewhere in this article there are two equations, the Thomson relations, also known as the Kelvin relations, relating the three thermoelectric coefficients.
Information Sources: