Ultraviolet Catastrophe
Definition
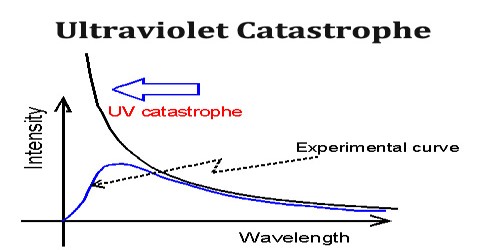
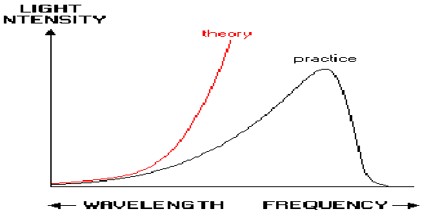
Ultraviolet Catastrophe refers to a paradox that emerged in scientists’ understanding of the way light is emitted by black bodies that exist in thermal equilibrium. It was also called the Rayleigh–Jeans catastrophe, was the prediction of late 19th century/early 20th century classical physics that an ideal black body at thermal equilibrium will emit radiation in all frequency ranges, emitting more energy as the frequency increases.
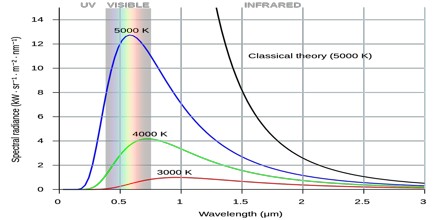
The name Ultraviolet Catastrophe was used to describe this failure of theory because UV light has a higher frequency than visible light. Obviously, the total energy output at any frequency is not infinite, a point made by Einstein and others. This would conflict with the law of conservation of energy.
The 19th-century understanding of physics reached an impasse around 1900 when it proved inadequate to explain the way light is emitted from objects. Under the classical model, an object in thermal equilibrium emits radiation of a given intensity at all possible wavelengths. As the frequency of the emitted light increases near the ultraviolet end of the spectrum, so do the wavelengths of light that must be emitted to match classical models. Eventually, the model predicts that black bodies should radiate infinite energy at high frequency. Since the first appearance of the term, it has also been used for other predictions of a similar nature, as in quantum electrodynamics and such cases as ultraviolet divergence.
Probem and Solution of Ultraviolet Catastrophe
Ultraviolet Catastrophe never caused any problems; its historical role is a late anecdote. It’s results from the equipartition theorem of classical statistical mechanics which states that all harmonic oscillator modes (degrees of freedom) of a system at equilibrium have an average energy of (1/2) kT.
According to classical electromagnetism, the number of electromagnetic modes in a 3-dimensional cavity, per unit frequency, is proportional to the square of the frequency. This therefore implies that the radiated power per unit frequency should follow the Rayleigh–Jeans law, and be proportional to frequency squared. Thus, both the power at a given frequency and the total radiated power is unlimited as higher and higher frequencies are considered: this is clearly unphysical as the total radiated power of a cavity is not observed to be infinite, a point that was made independently by Einstein and by Lord Rayleigh and Sir James Jeans in 1905.
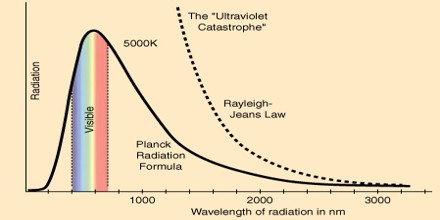
Planck derived the correct form for the intensity spectral distribution function by making some strange (for the time) assumptions. Albert Einstein solved the problem by postulating that Planck’s quanta were real physical particles—what we now call photons, not just a mathematical fiction. His photon had energy proportional to its frequency and also explained an unpublished law of Stokes and the photoelectric effect.