Introduction:
The wefts knitted fabrics have become comfortable and are in tune with the times. The present generation is grown-up with the permanent press and they are going to demand wrinkle free, ease-of-care fabrics. The recent success of knits has been greatly due to their easy care properties. The mobility of people, in general, has been increased due to facilities for quick transport. Travelers usually need carefree fabrics. And knitted fabrics do comply with this requirement, as they generally require no ironing and are, therefore, ideal for traveling persons. Also for swimwear and sportswear. Also knitting units require very less labor and hence all problems related with labor organization, wages, benefits to labor etc. are very much reduced in the weft knitting industry. So that people can get all these advantages with the knitted fabrics at comparatively low prices. Therefore it is necessary to study about the properties of weft knitted fabrics produced from different types of structure. Knitted fabrics structures are classified according to the arrangement of loops in their courses and Wales. Four primary structures are Plain, Rib, Purl, and Interlock. Here we will study about the 1´1 Rib, 1´1 Skeleton rib, 2´2 English rib, 2´2 Swiss rib, 6´3 Derby rib fabrics properties produced from 100% Cotton combed yarn (20/2Ne, 32/2Ne). Tested properties are courses/cm, Wales/cm, stitch density, stitch length, GSM, tightness factor, dimensional stability.
Effect of Fabric Structure on Rib Properties
Structure of rib fabric is most important factor for rib fabrics properties. Different structure show different value for wales per cm, course per cm, Stitch length, Stitch density, Tightness factor, GSM, Dimensional stability if the same yarn and machine setting are used. Fabrics sample were knitted at the V-bed knitted machine (keeping the yarn tension, take down tension value, gauge value constant), 14 Gauge and 40 inch width.
Different rib structure is produced by increasing or decreasing no of active needle in knitting. When Increase of the no. of active needle in knitting the fabric shrinkage and extension percentage is reduced and also affect the other knitted fabrics properties. In this project we find out effect of fabric structure on rib fabric properties we study about the comparison between different structures.
Methodology
For the study of “Effect of fabric structure on Rib fabric properties”, five rib fabric 1×1 Rib,1×1 Skeleton Rib, 2×2 Swiss Rib, 2×2 English Rib, 6×3 Derby Rib were produced. On each sample the following test parameters were measured.
- Wales per 3cm
- Course per 3cm
- Stitch density
- Stitch length
- Tightness factor
- GSM
- Dimensional stability
Limitation:
In this project work we faced the following limitations:
- In a short time we complete this project work.
- It will better if we submit more statistical analyzed data.
- It will better if we collect yarn at the start of the project work.
- It will better if we produce more sample structure.
- We work with 10 data for each fabric property. It will better if we work with more data.
- We could not get more time to revise our data three more times. So it is not impossible that, some mistake in the data table
Literature Review
Introduction:
The contribution of knitwear in textile sector export has shown phenomenal growth during the recent years. The knitted fabrics are very soft, elastic, absorbent, and durable having wonderful adaptability and are available at comparatively low prices. Despite of all these advantages there are certain quality limitations connected with the knitted fabrics.
Fabric structure and property:
In garment length knitting, a direct change of knitting from 2×2 and 1×1 rib brings every third needle into action. At the first course, the limbs of the loops knitted on these formerly empty needles open out, producing apertures between every two wales that spoil the appearance of the structure. This problem is overcome by knitting a tubular cover course of plain on all needles in one bed, then on all needles in the other bed. On each side, the sinker loops draw the wales together and prevent the loops on the newly- introduced needle from forcing the wale apart.
1×1 rib is alternately balanced by alternate wales of face loops on each side; it therefore lies flat without cut when cut. It is more expensive fabric to produce than plain and is a heavier structure; the rib machine also requires finer yarn than a similar gauge plain machine. Like all weft knitted fabrics, it can be unroved from the end knitted last by drawing the free loop heads through to the back of each stitch it can be distinguished from plain by the fact that the loops of certain wales are withdrawn in one direction and and the others in opposite direction, whereas the loops of plain are always withdrawn in the same direction, from the technical face to the technical back
Experimental decision:
- Wales per cm increase with the increase of no of active needle in knitting.
- Course per cm increase with an increase in loop length.
- Wales per cm decrease with an increase in loop length.
- Loop length increases after wet relaxation process when compared to that of the value set in the machine.
- Thickness of fabric increase with an in increase in loop length.
- Shrinkage produced in the direction of wale and course wise extension is occurring.
- From the study, it is found that the shrinkage and extension percentage increases with the increase of needle drop.
Raw Material
Cotton today is the most used textile fiber in the world.
Its current market share is 56 percent for all fibers used for apparel and home furnishings and sold in the U.S. [1]. Another contribution is attributed to nonwoven textiles and personal care items. It is generally recognized that most consumers prefer cotton personal care items to those containing synthetic fibers. World textile fiber consumption in 1998 was approximately 45 million tons. Of this total, cotton represented approximately 20 million tons. [2]. The earliest evidence of using cotton is from India and the date assigned to this fabric is 3000 B.C. There were also excavations of cotton fabrics of comparable age in Southern America. Cotton cultivation first spread from India to Egypt, China and the South Pacific. Even though cotton fiber had been known already in Southern America, the large-scale cotton cultivation in Northern America began in the 16th century with the arrival of colonists to southern parts of today’s United States. [3] .The largest rise in cotton production is connected with the invention of the saw-tooth cotton gin by Eli Whitney in 1793. [4] With this new technology, it was possible to produce more cotton fiber, which resulted in big changes in the spinning and weaving industry, especially in England
Introduction:
Kinds and types of cotton
Scientific Name of cotton
(i) Gossypium Herbaceum
(ii) Gossypium Arboreum
(iii) Gossypium Hirsutum
(iv) Gossypium Barbedense
Different kinds and types of cotton are grown in various parts of the world. Variation among cotton fibers occurs because of growth conditions including such factors as soft, climate, fertilizers, and pests. The quality of cotton fiber is based on its color, staple, fineness, and strength. Usually, the longer fibers are finer and stronger. The particular kind of cotton is often identified by the name the country or geographical area where it is produced. Though many species of cotton are grown commercially, they may be conveniently divided into three types.
- Type 1 fibers have staple lengths (i.e. average fiber length) varying from 25 to 60 mm, including high quality fine cottons such as the Egyptian, Sudanese and Sea Island varieties.
- Type 2 fibers are coarser species, which form the bulk of the world crop with shorter lengths (about 13-33mm) such as American Upland cotton.
- Type 3 fibers are of still shorter staple length (about 9-25mm) commonly produced in various Asian countries.
Major cotton producers at the present time are China, the USA, India, Pakistan, Uzbekistan; other countries producing small but not insignificant quantities include Brazil, Turkey, Mexico, Egypt, and Sudan. At present the four largest exporters of cotton in the world are USA, Uzbekistan, Franc-zone Africa and Australia. The major high quality cotton fiber classes are listed below:
1.American Upland cotton fibers: They are fairly white, strong, and dull, and range in staple length from 22-32 mm. The Upland cottons are usually categorized as short staple, medium-staple, and long staple. The short staple are less than 25 mm and are produced in Oklahoma and central and West Texas. The medium-staple cotton is 25-28 mm in length are produced in Southeast, the MississippiValley, and the low valleys of Arizona and California. The long staple cottons are 29 mm or longer and are grown in the high altitude areas of the Southwest. The cotton grown in the San Joaquin valley of California has a staple length from 28-29 mm and is stronger than the other Upland kinds.
2.American Pima cotton fiber: It is fine, strong, lustrous, silky and creamy-brown-white in color. The fiber has the staple length from 35-38 mm. American Pima fiber is used for primarily for sewing thread and also used in high-quality broad cloth and other fabrics where silky smoothness, softness, and luster are desired.
3.Egyptian cotton fibers: They are light brown, fine strong and 32-38 mm in length. They are used in the same application as American Pima.
Cotton grading
American Cotton Grading:
The grading of American upland cotton is based upon three main characteristics: color, trash content or foreign, and preparation. It is important to note that staple length is not one of the three. The color may be referred to as extra white, white, spotted, tinged, and yellow stained, in decreasing order of merit. The variety, weather, sofl, picking,efficiency, and so on, governs, the color. The main eight American cotton grades are given below:
i. Middling fair
ii. Strict good middling
iii. Good middling
iv. Middling
v. Strict low middling
vi. Low middling
vii. Strict good ordinary
viii. Good ordinary
Indian Grading:
- Super Choice
- Choice
- Super fine
- Fine
- Fully good
- Good
- Fully good fair
Egyptian Grading:
- Extra fine
- Fine
- Good
- Fully good fair
- Good fair
- Fair
Characteristics of cotton
Cotton, as a natural cellulose fiber, has a lot of characteristics, such as;
- Comfortable Soft hand
- Good absorbency
- Color retention
- Prints well
- Machine-washable
- Dry-cleanable
- Good strength
- Drapes well
- Easy to handle and sew
Uses of cotton
- Apparel – Wide range of wearing apparel: blouses, shirts, dresses, childrenswear, active wear, separates, swimwear, suits, jackets, skirts, pants, sweaters, hosiery, neckwear.
- Home Fashion – curtains, draperies, bedspreads, comforters, throws, sheets, towels, table cloths, table mats, napkins
Structure and properties of cotton fibers
Fiber structure and formation
The botanical name of American Upland cotton is Gossypium Hirsutum and has been developed from cottons of Central America. Upland varieties represent approximately 97% of U.S. production [4].
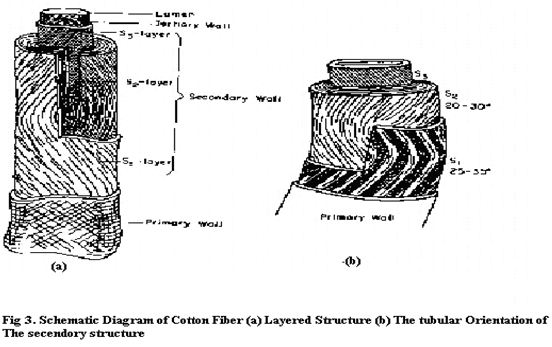 Fiber structure and formation
Fiber structure and formation
The botanical name of American Upland cotton is Gossypium Hirsutum and has been developed from cottons of Central America. Upland varieties represent approximately 97% of U.S. production [4].
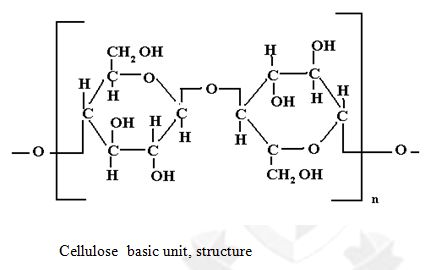
Each cotton fiber is composed of concentric layers. The cuticle layer on the fiber itself is separable from the fiber and consists of wax and pectin materials. The primary wall, the most peripheral layer of the fiber, is composed of cellulosic crystalline fibrils. [9] The secondary wall of the fiber consists of three distinct layers. All three layers of the secondary wall include closely packed parallel fibrils with spiral winding of 25-35o and represent the majority of cellulose within the fiber. The innermost part of cotton fiber- the lumen- is composed of the remains of the cell contents. Before boll opening, the lumen is filled with liquid containing the cell nucleus and protoplasm. The twists and convolutions of the dried fiber are due to the removal of this liquid. The cross section of the fiber is bean-shaped, swelling almost round when moisture absorption takes place.
The overall contents are broken down into the following components.
Raw cotton components:
| 80-90% | Cellulose |
| 6-8% | Water |
| 0.5 – 1% | Waxes and fats |
| 0 – 1.5% | Proteins |
| 4 – 6% | Hemicelluloses and pectin’s |
| 1 – 1.8% | Ash |
Repeat unit of cellulose
The current consensus regarding cellulose crystallinity (X-ray diffraction) is that fibers are essentially 100% crystalline and that very small crystalline units imperfectly packed together cause the observed disorder.
The density method used to determine cellulose crystallinity is based on the density gradient column, where two solvents of different densities are partially mixed. Degree of Crystallinity is, then, determined from the density of the sample, while densities of crystalline and amorphous cellulose forms are known (1.505 and 1.556 respectively). Orientation of untreated cotton fiber is poor because the crystallites are contained in the micro fibrils of the secondary wall, oriented in the steep spiral (25-30o)to the fiber axis.
The micro- structure of cotton –
Length – 1cm to 6.5cm (.5 to 2 inch).
Diameter – 11μm to 22 μm.
Convolutions – sixty per centimeter
Colour – generally white, may be creamy or brown.
Length width ratio – 6000:1 to 350:1
Light reflection – low luster, dull appearance.
Fibers properties
| Property | Evaluation |
| Shape | Fairly uniform in width, 12-20 micrometers; length varies from 1 cm to 6 cm (½ to 2½ inches); typical length is 2.2 cm to 3.3 cm (⅞ to 1¼ inches). |
| Luster | High |
| Tenacity (strength) Dry Wet | 3.0-5.0 g/d 3.3-6.0 g/d |
| Resiliency | Low |
| Density | 1.54-1.56 g/cm³ |
| Moisture absorption raw: conditioned saturation mercerized: conditioned saturation | 8.5% 15-25% 8.5-10.3% 15-27%+ |
| Dimensional stability | Good |
| Resistance to acids alkali organic solvents sunlight microorganisms insects | damage, weaken fibers resistant; no harmful effects high resistance to most Prolonged exposure weakens fibers. Mildew and rot-producing bacteria damage fibers. Silverfish damage fibers. |
| Thermal reactions to heat to flame | Decomposes after prolonged exposure to temperatures of 150˚C or over. Burns readily. |
Physical properties of cotton
Fiber length
Fiber length is described [7] as “the average length of the longer one-half of the fibers (upper half mean length)” This measure is taken by scanning a “beard ” of parallel fibers through a sensing region. The beard is formed from the fibers taken from the sample, clasped in a holding clamp and combed to align the fibers. Typical lengths of Upland cottons might range from 0.79 to 1.36in.
Cottons come from the cotton plant; the longer strand types such as Pima or SeaIsland produce the finest types of cotton fabrics [18].
Length uniformity
Length uniformity or uniformity ratio is determined as ” a ratio between the mean length and the upper half mean length of the fibers and is expressed as a percentage”[7]. Typical comparisons are illustrated below.
Low uniformity index shows that there might be a high content of short fibers, which lowers the quality of the future textile product.
| LENGTH UNIFORMITY | UNIFORMITY INDEX [%] |
| Very High | >85 |
| High | 83-85 |
| Intermediate | 80-82 |
| Low | 77-79 |
| Very Low | <77 |
Fiber strength
Fiber strength is measured in grams per denier. It is determined as the force necessary to break the beard of fibers, clamped in two sets of jaws, (1/8 inch apart) [7]. Typical tensile levels are illustrated. The breaking strength of cotton is about 3.0~4.9 g/denier, and the breaking elongation is about 8~10%. [20]
| DEGREE OF STRENGTH | FIBER STRENGTH [g/tex] |
| Very Strong | >31 |
| Strong | 29-30 |
| Average | 26-28 |
| Intermediate | 24-25 |
| Weak | <23 |
Micronaire
Micronaire measurements reflect fiber fineness and maturity. A constant mass (2.34 grams) of cotton fibers is compressed into a space of known volume and air permeability measurements of this compressed sample are taken. These, when converted to appropriate number, denote Micronaire values.
| COTTON RANGE | MICRONAIRE READING |
| Premium | 3.7-4.2 |
| BaseRange | 4.3-4.9 |
| DiscountRange | >5.0 |
Color
The color of cotton samples is determined from two parameters: degree of reflectance (Rd) and yellowness (+b). Degree of reflectance shows the brightness of the sample and yellowness depicts the degree of cotton pigmentation. A defined area located in a Nickerson-Hunter cotton colorimeter diagram represents each color code. The color of the fibers is affected by climatic conditions, impact of insects and fungi, type of soil, storage conditions etc. There is five recognized groups of color: white, gray, spotted, tinged, and yellow stained. As the color of cotton deteriorates, the process ability of the fibers decreases.
Trash
A trash measurement describes the amount of non-lint materials (such as parts of cotton plant) in the fiber. Trash content is assessed from scanning the cotton sample surface with a video camera and calculating the percentage of the surface area occupied by trash particles. The values of trash content should be within the range from 0 to 1.6%. Trash content is highly correlated to leaf grade of the sample.
Leaf grade
Leaf grade is provided visually as the amount of cotton plant particles within the sample. There are seven leaf grades (#1-#7) and one below grade (#8).
Preparation
Preparation is the classer’s interpretation of fiber process ability in terms of degree of roughness or smoothness of ginned cotton.
Extraneous matter
Extraneous matter is all the material in the sample other than fiber and leaf. The classer either as “light” or “heavy” determines the degree of extraneous matter. NEPS
A nep is a small tangled fiber knot often caused by processing. Neps can be measured by the AFIS nep tester and reported as the total number of neps per 0.5 grams of the fiber and average size in millimeters. Nep formation reflects the mechanical processing stage, especially from the point of view of the quality and condition of the machinery used.
Chemical properties of cotton
Effect of –
- Acid: Weaken and destroyed hydrolise the glucoside oxygen atom, concentrate Nitric acid, for short time, causes some shrinkage and increase strength and dye-ability.
- Alkali: normally resistance, when boiled in presence of O2 , oxycellulose form, treating with 20 percent NaOH increase strength and dye ability, process is called Mercerization. Liquid ammonia etc.
- Bleach-All kinds, NaOCl and Na Per borate are common H2O2 is least harmful.
- Organic Solvent – resistance. So dry wash is possible.
- Heat – conductive ironing temp – 1500 c, Decompose 24000 c, Ignition temp – 3900 c.
- Sun light- Affected by infrared cause deteriorates colour becomes yellow.
- Dye-ability – Azoic, Direct, Reactive, sulphur and Vat dye.
- Attack by moth – No
- Attack by mildew – Untreated not easily but starches and gums increase activity.
Critical temperatures
- Favorable travel temperature range – below 25 °C (77 °F)
- Optimum travel temperature: 21 °C (70 °F)
- Glow temperature: 205 °C (401 °F)
- Fire point: 210 °C (410 °F)
- Autoignition temperature: 407 °C (765 °F)
- Autoignition temperature: (for oily cotton): 120 °C (248°F)
Cotton dries out, becomes hard and brittle and loses all elasticity at temperatures above 25°C (77°F). Extended exposure to light causes similar problems. A temperature range of 25 °C (77 °F) to 35 °C (95°F) is the optimal range for mold development. At temperatures below 0°C (32 °F), rotting of wet cotton stops. Damaged cotton is sometimes stored at these temperatures to prevent further deterioration.
Fiber processing
About 30% of world cotton machines harvest production. Australia, Israel and USA are the only countries where all cottons are picked by machines. Fifteen percent of world cotton production is ginned on roller gins and almost all rest of cotton is saw ginned in most countries [14].Cotton fibers in nonwovens are generally used in their bleached form. A lot of research and development has taken place for the efficient production of bleached fibers. The Kier bleaching process produces most of the bleached cotton fibers. Since cotton of lesser grades is useful for nonwovens, a conventional cleaning system does not suffice. This might include a coarse wire carding, called Cotton Master Cleaners, for cleaning the cotton.
Spinning and its principle
Most of the fibers produced for textile materials are processed into yarns. The principle of the conventional yarn manufacturing method is to introduce a twist into yarn-by-yarn revolution. One revolution gives just one turn of twist. This process is called spinning.
Knitted fabric properties
1. Wales /cm:
Wales is the column of loops along the length of the fabric. Wales determine the width of the fabric and are measured as wales per centimeter. The no. of wales per centimeter is called wales/cm. It is measured along the course direction by using counting glass and needle.
- When loop transfer occurs it is possible to transfer a wale A to another B and to recommence knitting with the second needle in which case more than one needle will have produced intermeshed loops in the same wale.
- In warp knitting a wale can be produced from the same yarn if the same guide laps the same needle at successive knitting cycles.
- Wales are connected together across the width of the fabric by sinker loop (weft knitting)or under laps(warp knitting).
- Wales show most clearly on the technical face and technical back of single needle bed fabric.
- For single jersey fabric Wales show on face side as V shape and from back side as half circle
Course/cm:
A course is a predominantly horizontal raw of needle loops produced by adjacent needle during the same knitting cycles. Course is a row of loops across the width of fabric. A course determines the length of fabric and is measured as course per centimeter .
The number of course per centimeter is called course/cm. it is measured along the wale direction by using counting glass and needle.
2.Stitch density:
The term stitch density is frequently used in knitting instead of a linear measurement of courses or wales. It is the total number of needle loops in a square measurement such as a square inch or square centimeter. It is obtained by multiplying the number of courses and wales per centimeter together. Stitch density tends to be more accurate measurement because tension acting in one direction in the fabric, for example, procedure a low reading for the course a high reading for the wales, which then multiplied together cancel the effect out. Usually pattern rows and course are, for convenience, considered to be synonymous when counting course per unit of linear measurement.
Stitch density = wales per cm(wpcm) ×course per cm(cpcm)
3.Stitch length.
The length of yarn knitted in to one stitch in a weft knitted fabric. Stitch length is theoretically a single length of yarn which includes are needle loop and half the sinker loop on either side of it. Generally the larger the stitch length the more extensible and lighter the fabric and poorer the cover, capacity and busting strength.
Stitch length = one needle loop + two half a sinker loop
Stitch length can be determined by a HATRA (Hosiery and Allied Trade Research Association England) courses length tester.
The HATRA courses length tester is simple apparatus consisting of a rectangular board on which scales are marked in inches and cm along the longitudinal axis. A small clamping weight of about 10 gm is provided to remove the crimp from the yarn. To measure the stitch length marking is made at a distance of 50 wales and each courses unraveled carefully from the fabric and measured. About 20 to 30 courses can be measured this fashion to arrive at the average stitch length of 50 loops. This average length is then by 50 to get the divided stitch length.
4.Tightness factor:
Munden first suggested the use of a factor to indicate the relative tightness or looseness of plain weft knitted structure, to be used in a similar manner to that of the cover factor in the weaving industry. Originally termed the cover factor but now referred to as the tightness factor (TF), he defined if as the ratio of the area covered by the yarn in one loop to the occupied by that loop. The total area covered by yarn is: s×l×d
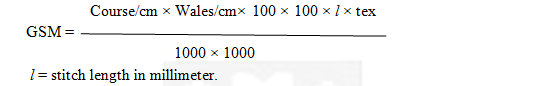
For single jersey fabrics: K.S values lie between 1.29 to 1.64, mean K=1.47. For most weft knitted structures (including S/J, D/J and wide range of yarns): 1≤ K≤ 2, mean K=1.5
The tightness factor is very useful in setting up knitting machines. At mean tightness factor, the stain in yarn, machine and fabric is constant for a wide range of conditions.
5.GSM:
Weight per unit area can be measured by a portable balance by cutting the fabric in 10″×10″ with the template or by calculation with the formula:
GSM =(Course/cm × Wales/cm× 100 × 100 × l × tex)/1000 × 1000
l = stitch length in millimeter.
The result is expressed in gm/sq.meter, popularly known as GSM.
GSM or weight per unit area of fabric is an important property that is again related to a host of their properties. The weight is determined by two factors that interact the loop size and the yarn size. The effect of loop size is simple express. If the sizes of the yarn remain constant, then increase the loop size produce a decrease of weight per unit area.
6.Dimensional Stability:
The ability of a fabric to retain its dimensions when exposed to use and or an ageing process to water, washing, steaming, drying or other process is called dimensional stability.
In other word, changes in length and or width of a fabric when subjected to specified conditions. It may be extension and shrinkage or relaxation, both length and width direction.
Relaxation:
Knitted fabrics tend to change dimension in width and length after being taken off the machine even without yarn shrinkage indicating a change of loop shape rather than of loop length. During knitting the loop structure is subjected to a tension of approximately 15-25 grams per needle from source as the take down mechanism and in the case of fabric machines, the width stretcher board. Unless the structure is allowed to relax from its strain and distorted state at sometime during manufacturing the more favorable conditions for fabric relaxation provided during washing and wearing will result in a change of dimensions leading to customer dissatisfaction.
Relaxation test can be carried out on fabric as a routine procedure or as spot check on suspect deliveries. There are British Standard procedures for relaxation testing and some of the large retail/whole sales purchasers have established tests of their own. Most test procedures involves by measurement under water and or spinning and tumble drying.
Extension:
Extensibility is a peculiar characteristic of knitted fabric. However, the amount of extensibility expected of a fabric depends on the end use. For example, extensibility of a double knitted fabric needs to be low for many of the uses to which the fabrics are put to, sometimes garments makers also stipulate requirements for fabric extensibility. Usually an extension tester is used two jaws in the machine. A uniform weight is applied to the fabric and the percentage extension is measured by using the formula.

Rib Fabric Structure
1.0Introduction
The first rib frame was invented by Jedediah Strutt of Derby in 1755, who used a second set of needles to pick up and knit the sinker loops of the first set. It is now normally knitted with two sets of latch needles (Fig – 1, and Fig – 2); Rib has a vertical cord appearance because the face loops show a reverse loop intermeshing on the other side. 1×1 rib has the appearance of the technical face of plain on both sides until stretched to reverse loop wales in between. A rib fabric is defined as a fabric in which all the loops in any individual wale are either knit or purl, it cannot have both in the same wale. The fabric is the same on both sides, therefore it is a balanced fabric which is stable. Rib fabric lies flat without edge curl. The main characteristic of rib fabric is it’s horizontal extensibility.
The rib structure causes the fabric to concertina and pull in, with the result that stitch for stitch a rib fabric has a narrower width than a plain fabric, but can extend to the same width as the plain fabric. Rib structures are good for welts and close fitting garments. They can be composed of any combination of knit or purl wales1x1, 2×2, 2×3 and so on.
2.0Rib structure
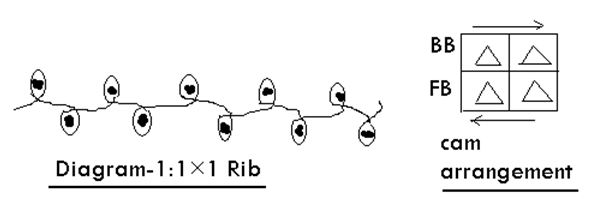
2.1 1×1 Rib
The simplest rib fabrics is. It is normally knitted with two sets of latch needles (Diagram-
4). Rib has a vertical cord appearance because the face loop Wales tend to move over and in front of
the reverse loop intermeshing on the other side, 1×1 rib has the appearance of the technical face of plain fabric on both sides until stretched to revel
the reverse loop Wales in between.1×1 rib production of by two sets of needles being alternately set or gated between each other. Relaxed 1×1 Rib is theoretically twice the thickness and half erable stretch. In practice, 1×1
rib normally relaxes by approximately 30 percent compared with its knitting width.1×1 rib is balanced by alternately wales of face loops on each side; it therefore lies flat without curl when cut. It is a more ex -pensive fabric to produce than plain and is a heavier structure.1×1 rib shown in diagram-1;
2.2 1×1 Skeleton rib
It is possible to produce Skeleton 1×1 rib on V-bed knitting machine by taking every third needle from both bed out of action. Skeleton 1×1 rib shown on Diagram-2.
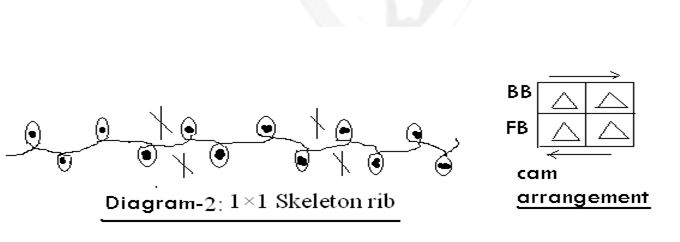
2.3 2×2 Swiss rib
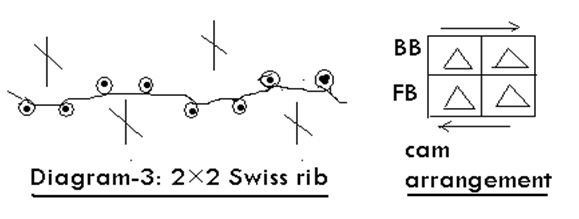
2×2 Swiss rib (Diagram-3), this is produced on a rib machine by taking one needle out of action opposite the two needles knitting. Swiss rib is something confusingly termed 2/3 rib because 2 out of 3 needles in each bed are knitting. It is not possible to commence knitting on empty needles with the normal 2×2 arrangement because the two needles in each bed will not form individual loops – they will make one loops across the two hocks.
2.4 2×2 English rib
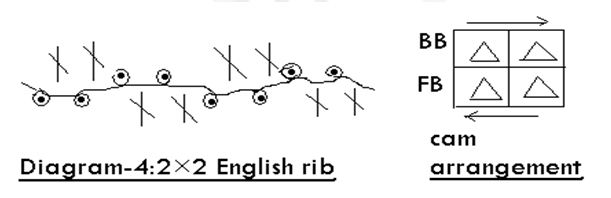
2×2 English rib is shown on Diagram-4. English rib is produced on a purl machine or rib machine with two empty tricks opposite to the two needles knitting; this type of rib is less elastic it is possible to produce on V-bed knitting machine.
2.5 6×3 Derby Rib
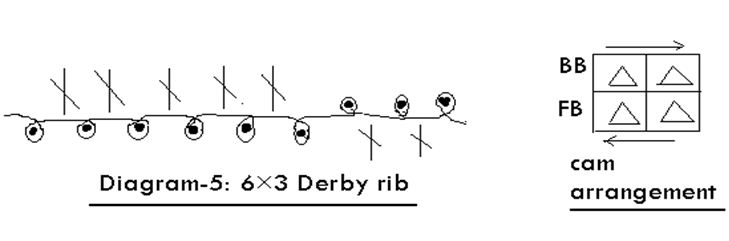
It is possible to produce 6×3 Derby Rib on V-bed knitting machine. It is produced by six needle in action and two needle out of action in front bed , alternately five needle out of action and three needle in active in bed.
3.0Feature and properties of Rib Fabric
- It is a reversible structure, i.e. face and back side has same appearance in 1×1, 2×2, 3×3 ribs etc. the appearance shows vertical cords and thin ridges, in between.
- 1×1, 2×2, 3×3 ribs etc. are balanced structures because of alternate number of face and reverse Wales in each side.
- It is heavier and thicker structure than the plain knit structure with similar gauge used for plain-knit and rib structure.
- It requires a knitting machine with cylinder and dial and two sets of needle-cylinder needles and dial needles.
- Rib structure cannot be unroved from the course knitted first because sinker loops are securely anchored by the cross-meshing between face and reverse loop Wales. It can be unroved from the last course knitted.
- As mentioned earlier, it has the maximum extensibility in width way and hence rib trimmings are most suitable for neck bands, collars, arm bands, sleeve cuff bands in sweater knitting and for tops of socks, as they fit tighter to the body than the plain knit give a smart appearance.
- Rib fabrics are extensively used in the production of outerwear garments in western world.
- The fabric does not curl at the edges due to its balanced nature. This is property of rib structure is particularly useful in cutting and sewing operations.
- The structure is more opaque than a jersey and hence this structure is used for swimwear.
4.0 Uses of Rib fabric
Rib is particularly suitable for the extremities of articles such as tops of sock, cuffs, sleeves, rib borders of garments and stocking and strapping for cardigans. It is knitted at the tops at the tops of plain knit socks and gloves.
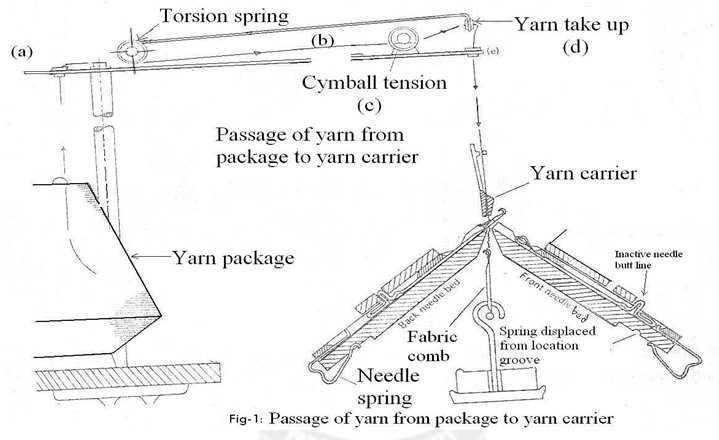
Machine description
1.0Introduction
V – Bed knitting machine is the most versatile weft knitting machines. V- bed knitting machine has two stationary needle beds arranged in an vertical V forma -tion. Latch needles and others slide in the tricks during the knitting action. Their butts project and are controlled as they pass through the tracks formed by the angu
-lar cams of a bi-directional cam system. It is attached to the underside of a carriage that, with its selected yarn carriers, traverses in a reciprocating manner ac
-cross the machine width. There is a separate cam system for each bed, the two sy
-stem are linked together by a bow,or bridge, that passes across from one needle bed to other. The cam systems for each needle bed are symmetrically arranged so that knitting, and in some cases loop transfer, may be achieved in either direction of carriage traverse.
2.0Machine Specification
1) Type: Flate knit
2) Company Name: Exse Company Ltd.
3) Origin: Made in India
4) Machine width: 40 inch
5) Machine gauge: 14
3.0The yarn carriers arrangemen
The yarn carriers are arranged to slide
On both sides of double prismatic guiding bars and there are usually six or seven carriers operate on the same track of the same bar, it is essential to arrange the sequence so that if the two carriers are deposited on the same side, the one nearest to the cam-carriage will be the one first required to traverse back in the opposite direction.
There are two methods of entraining carriers with cam systems on double system machines; uncrossed and crossed arrangement, the same yarn carriers operate with the same cam systems in both directions of traverse. This simplifies the control and is essential when two carriers are on the same track, but it causes problems with vertical yarn floats at the selvedges because the yarn with the leading cam system will finish the first course but will not knit the return traverse.
With the crossed arrangement, one yarn carrier will always be entrained with the leading cam system and the other with the trailing cam system, so that if the carriers have different colored yarns, each will knit alternate courses.
In carrier positioning and traversing for jacquard (fig.1), the yarn carriers must be carefully positioned initially in order to keep their number to minimum whilst ensuring that empty traverses (without knitting a course) are avoided whenever possible, as they reduce productivity. By drawing a plan of traverses and colors, and indicating each time a new yarn is picked-up, the initial positions can soon be established. For double system knitting in two or three color jacquard, each system will require as many carriers as there are colors, but two color jacquard is necessary to after the seq
4.0Cam system of V – Bed knitting machine
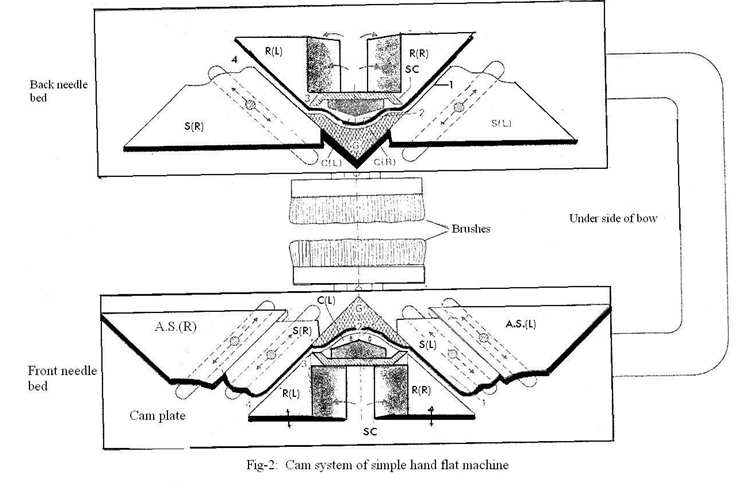
4.1 Stitch cam settings
The stitch cams are located in slots by studs and they may be raised or lowered to a different setting position by moving the stud along the slot (Fig.2). Unless the rate of yarn of yarn feed is controlled, the setting of the stitch cam at knock-over
will determine the stitch length because it controls the distance the head of the needle mine the stitch length because it controls the distance the head of the needle descends below the knock-over bits edge from the rest position. The alternating stitch cam settings are indicated by pointers on a calibrated scale on the outside of the cam-plate.
On hand flats, the adjustment of the setting is obtained by hand controls, whilst on modern electrically-controlled flats. Each stitch cam is raised and lowered by its own step motor. So wide range lengths can the achieved during the knitting of garment.
4.2 Spring–loaded cams
Raising cams (R) and cardigan cams (C) (Fig.2) are of the spring-loaded type that can be depressed into the under-surface of the cam-plate against the action of a spring. The leading edge of a leading raising cam is straight so that it causes the butts so follow its profile. However, the trailing inner edge of the cam, which is the leading edge when that cam is trailing inner edge of the cam, depressing the cam into the cam-plate and then follow an undisturbed path across its face. After the butts have passed, the cam spring outwards from the cam-plate to resume its active position for the return traverse.
On hand flat machines, the cams are often of the sinkable setting type so that they can be set either.
a. fully in action out from the cam-plate so that they act on every needle butt,
b.partly withdrawn into the cam-plate so that they miss the low (short) butts, pass
undisturbed across their surface, or
c.Fully withdrawn into the cam-plate so that all butts pass undisturbed across their
surface.
The standard set-out when using different lengths of the butts is two long and one short in each bed, with the short butt centered between the two long butts in the opposite bed. This is enables changes from 1×1 to 2×2 rib knitting to occur.
Changes of cam setting are achieved by the movement of control that are placed on the outside of the cam-plate. In the case of mechanical automatic power flats, these controls can consist of metal push sides, each corresponding to a different cam whose sideways movement produces the required change of cam setting. At each end of the machine is contact post containing striking plates, aligned to contact the sides as the carriage reaches the end of its traverse so that the cams may be set for the return traverse. Control of the plates is achieved from the main garment (machine) control of the machine.
Electronic machines have continuous electronic contact with the cam carriage and therefore do not require the cam slide arrangement.
On hand flat machines it is useful to have split cardigan cams so that a different setting can be achieved in each direction without having to stop the carriage at the end of each traverse.
The automatic machine can change the cam setting for each traverse; split cardigan camming is unnecessary and these machines usually have a single cardigan cam for both traverse directions.
Two or more cam systems
Although hand flat machines have single cam carriages, many automatic power flat machines have two, three or four cam systems, each with a complete set of knitting cams arranged side by side in the same cam-plate each working with a separate yarn carrier. Thus, in one cam carriage traverse, as many courses as there are cam system can be knitted.
However, compared with a single system machine, the rate of carriage traverse is often reduced, firstly because of the heavier carriage, and secondly because it is longer and must traverse further, thus making the machine longer. There is also a problem of vertical floating threads at the selvedge edges of the machine construction, together with the use of lightweight alloys and automatic thread cutters have largely overcome these problems.
Split cam-carriages
Another useful development is the split cam-carriage. For example, a double system cam carriage operating across the full width might also be split into two single systems (2×1) cam-carriages, each covering half the needle bed or both co-operating in the knitting of wedge-shaped or other complex designs. Split cam-carriage machines have been built with a total of two (2×1), four (2×2), six (2×3), and even eight (2×4) systems.
5.0 The knitting action of the V-bed hand flat machine
Numbers 1 to 4 below correspond to the numbers in the knitting action illustrations (Fig. 3), assuming a carriage traverse, using the cams given an (L) designation to provide the positive movements.
- The Rest Position: The tops of the heads of the needles are level with the edge of the knock-over bits. The butts of the needles assume a straight line until contracting the raising cams R (R) because the leading stitch cams S and AS (L) are lifted to an inactive position. The lifting action is an alternating action that always lowers the trailing stitch cams in each system as the traverse commences. This action prevents needles from being unnecessarily lowered and a strain being placed on the old loops prior to the start-up of the knitting action.
- Clearing: The needle butts are lifted as they contact the leading edge of cams R (R). Which rises the needles to ‘tucking in the hook’ height with the under surface of cams (S) acting as guard cams. The needles are lifted to full clearing height as their butts pass over the top of cardigan cams C (R) and C (L).
- Yarn feeding: the yarn is fed as the needles descend under the control of guard cam (G). the required loop length is drawn by each needle as it descends the stitch cam S (R).
4. Knocking-over: To produce synchronized knocking-over of both simultaneously, the stitch cam S (R) in the front system is set lower than the auxiliary stitch cam AS (R), so that the latter is rendered ineffective. If, however. Delayed timing of the knock-over is employed, knock-over in the bed will occur after knock-over is employed in the back bed. In this case, stitch cam S (R) is not set as low as A.S.(R) (Number 5 in Fig.3) so that the depth setting of the latter cam produces the knock-over action. Delayed timing is only normally used on gauges finer than 8 npi and cannot be used for broad ribs.
Sample Production
1.0Introduction
V – Bed knitting machine have two rib gated, diagonally, approaching needle beds, set between 90 and 104 degrees to each other, giving an invert V – shape appearance.
Two sets needle are used for two beds. In rib fabric both side technical face appearance are shown.
2.0Requirement of sample
We selected the following structure for this project work
- 1×1 rib,
- 2×2 Swiss rib,
- 2×2 English rib,
- 1×1 skeleton rib,
- 6×3 Derby rib
Yarn requirements
We selected the following yarn for this thesis work
- Yarn Count : 20/2 & 32/2 Ne
- Fibre composition : 100% cotton fibre
- Ring or rotor : Ring yarn
- Carded or combed: combed
- TPI : 18 for 20/2 Ne and 20 for 32/2 Ne.
Machine requirements
| Types of structure | No of active needle for a repeat |
| 1×1 rib | 2 |
| 2×2 Swiss rib | 4 |
| 2×2 English rib | 4 |
| 1×1 skeleton rib | 8 |
| 6×3 Derby rib | 9 |
- No of active needle
For a repeat
5.0 Production process of rib fabric
Yarn package placing
(required count of yarn are placed on the creel)
↓
Fabric holding
(Generally the fabric are holding for new production,
after creeling the old and new yarns are nothing each with other).
↓
Needle set-up
(Needle are arranged on the needle bed
-according to the design of the fabric).
↓
Cam set-up
( after placing the needle the cam set on the machine).
↓
Stitch cam setting.
↓
Cam tension set-up.
TEST METHOD
Method of test for cotton weft knitted fabrics relevant to the starfish process control package
1. Principle
A fabric is relaxed by being subjected to one cycle of washing and tumble drying followed by four cycles of rinsing and tumbles drying. At the end of the specified procedure the fabric is defined as being in its “reference state”.
2.0 Apparatus
2.1 Front Loading Automatic Domestic Washing Machine (e.g. Hoover)
2.2 Domestic Tumble Dryer (e.g. Hoover).
2.3 Domestic Automatic Washing Powder (e.g. Persil).
2.4 Scales
2.5 Means For Providing The Standard Atmosphere For Testing Textiles Specified In.
B.S 1051 And 139, RH 65±2% at 200c±20c
3.0 Test Samples
3.1 Condition the test sample in the standard atmosphere for testing textiles (Ref.2.5)
until it has reached aquarium.
3.2 Sample for relaxation should be between 45cm and 75cm square and of single
thickness. Selvedges and/or crease marks should be avoided.
3.3 Sufficient specimens of appropriate dimensions should be prepared from the sample
to allow for those tests required to be made on reference state fabric to be carried
out according the appropriate methods.
[ N.B. Five specimens 70×70cm are usually sufficient.]
4.0Laundering
4.1 Wash Cycle
4.2 It is important to ensure that the first cycle of the relaxation procedure is a full
length hot wash with detergent to ensure thorough wetting of the specimen and
removal of loose dirt ,’ waxes and grease.
For domestic automatic washing machines this is achieved by using the 600C wash
cycle, international textile care labeling code 2.
Rinse Cycle
Subsequent cycle is designed through rewetting of the specimen before drying and
this can be conveniently achieved by using the rinse only cycle.
4.3 Sample load
It is important to maintain to a standard load weight in the washing machine.
Domestic automatic machines normally specify a recommended load for absorbent
materials, e.g. 2.75 kg for Hoover.
4.4 Washing powder
A normal domestic automatic powder which does not contain softener or fabric
conditioner can be used in the first full washing cycle. Use the quantity
recommended by the manufacturer.
5.Drying
To achieve the STARFISH reference state with reliability and consistency it is
essential that the test specimens are dry, i.e. contain only a minimum amount of
moisture (about 1%),on leaving the tumble dryer, the amount of moisture remaining
in a fabric can influence the extent of relaxation.
To ensure that this minimum reference state with reliability and consistency it is essential that the test specimens are dry, i.e. contain only a minimum a mount of moisture (about 1%),on leaving the tumble dryer, the amount of moisture remaining in a fabric can influence the extent of relaxation.
To ensure that this minimum moisture level is achieved it is necessary to determine the length of time required to bring the load to a constant dry weight prior to testing.
5.1.1. Drying time
Weight a standard conditioned load of specimens of either the same or similar construction to the sample load being tested or carry out a standard 600C hot with long spin (Ref.4.1).
5.1.2. On completion, transfer the load to the tumble dryer and tumble dry at the hottest
Temperature setting for a nominal period of time. e.g.60 minutes.
5.1.3. Remove load and weight of it.
5.1.4. Return load to the tumble dryer and continue tumbling at the highest temperature for a further 10 minutes.
5.1.5. Remove load and weight of it.
5.1.6. Repeat 5.1.4 and 5.1.5 until the weight of the washed and tumble dried load remains the same.
5.1.7. Drying time is the length of time taken to reach the stable weight plus 10 minutes cool down period, i.e. continue tumbling for 10 minutes with the heat turned off.
6. Test Procedure
6.1 Prepared the specimens as described in 3.0.
6.2 Weight the test specimen and where necessary up the load to the standard weight (e.g. 2.75 kg) with makeweights of similar construction and finish to the specimens being tested.
6.3 Place in the washing machine, add the recommended amount of washing powder to the dispenser and set the machine to wash at 600C with load spin (e.g. final speed at 800 rpm for 4 minutes.).
6.4 On completion of the wash cycle, transfer the load to the tumble dry at the highest temperature setting until dry (Ref.5.1).
6.5 On completion of the first tumble dry cycle return the load to the washing machine and using the rinse-only cycle,(including final speed at 800 rpm for 4 minutes), thoroughly re-wet the load. On completion return of time as was established in 5.1 and used in 6.4.
6.6 Repeat 6.5 three more times.
6.7 After completion of the full 5 cycles, condition the specimens in the standard atmosphere until they reached equilibrium.
6.8 Test specimens are now defined as in the STARFISH reference state.
Number of Visible Course and Wales per 3 Centimeters in a Weft Knitted Fabric
1. Principle
The number of face courses and wales visible within a minimum measuring distance
are counted. the result if expressed as courses or Wales per 3 cm.
2.0Apparatus
2.1 counting glass
2.2 means for providing the standard atmosphere for testing textiles specified in
B.S.1051 and ISO 139.RH 65% ± 2% at 200C ± 20C.
3.0 Test samples
The test samples should be sufficiently large to enable courses and wales to be
counted at 10 different places over a minimum measuring distance of 3 cm spaced to
give good representations of the sample avoiding selvedge and/or centre creases.
4.0 Test procedure
4.1 condition the test sample in standard atmosphere for testing textiles (Ref.2.2) until it
has reached equilibrium.
4.2 Lay of the sample on a flat horizontal surface, removing wrinkles with
without stretching. Position the edge of the counting glass so that it is either parallel to or perpendicular to the line of wales. Courses are counted perpendicular to the wale line. Count the number of courses and wales per 3 cm. repeat 4.3 at nine different places on the sample. Giving a total of 10 determinations for courses and 10 determinations for wales.
5.0 Calculation of results
5.1 Calculate the mean and % accuracy for courses and wales per 3 cm
from the measurements.
Report results per 3 cm correct to 1 decimal place.
N.B. If courses and wales per cm are required, divide each determination by 3 and
calculate the mean and % accuracy. report results per cm correct to 1 decimal place.
Length density of yarn taken from a weft knitted fabric
1. Principle
Lengths of yarn are removed from the sample and their mass determined. The straightened lengths of a proportion of them are determined and the total length calculated. The linear density of yarn in a unit of the tex system is then calculated.
2.0 Apparatus
2.1 Crimp tester.
2.2 Counting glass.
2.3 Analytical balance.
2.4 Scissors.
2.5 Means for providing the standard atmosphere for testing textiles specified in
B.S.1051 and ISO 139.RH 65% ± 2% at 200C ± 20C.
3.0 Test samples
Test sample should be sufficiently large to enable100 stitches to be cut from one
Course in at least two different positions on the sample, avoiding selvedges and/or
centre creases.
4.0 Test procedure
4.1 Condition the test sample in the standard atmosphere for testing textiles (Ref.2.5)
until it reached equilibrium.
4.2 Lay the sample on a flat horizontal surface,removing wrinkles without stretching.
4.3 Make a cut along one wale of the sample,count 100 wales and make a second cut.
4.4 Remove a length of yarn from the cut position and record its length in mm at the correct tension on the crimp tester.
For yarn greater than 7 tex:
Tension= tex/5 + 4g
For yarns less then 7 tex: Tension = tex × 0.75g
4.5 Remove the further nine threads and retain with the measured length.
4.6 Repeat 4.4 and 4.5 a further four times making a total of 50 threads and five recorded length measurements.
4.7 Weight 4.3 to 4.7 on another part sample.
5.0 Calculation of Results
5.1 For each group of 50 threads the tex is calculated using the formula:
Txe=1000
l
Where W= Weight in grams.
l= total length in meters.
5.2 Calculate the mean and % accuracy of the two tex values.
5.3 Repeat results correct to 1 decimal place.
5.4 When English cotton count (Ne) is requested, calculate using the formula:-
5.5 Cotton count= 590.5/tex
Stitch length in weft knitted fabrics
A length of yarn by a known number of needles is taken from the sample and measured; stitch length is obtained by the calculation.
2.0 Apparatus
2.1 Crimp Tester
2.2 Counting Glass
2.3 Scissors.
2.4 Means For Providing The Standard Atmosphere For Testing Textiles Specified In
B.S. 1051 and ISO 139.Rh 65% ± 2% At 200c ± 20c.
3. Test Sample
Test sample should be sufficient large to enable 100 stitches to be cut from one course in at least two different positions on the sample, selvedges and/or centre creases.
4.0 Test procedure
4.1 Condition the test sample in the standard atmosphere for testing textiles (Ref. 2.4)
until it has reached equilibrium.
4.2 Lay the sample on a flat horizontal surface, removing wrinkles without stretching.
4.3 Make a cut along one wale of the sample, count 100 visible and make a second cut.
4.4 Remove a length of yarn from the cut position and record its length in mm at the correct tension on the crimp tester.
For yarn greater than 7 tex:
Tension= tex/5 + 4g
For yarns less then 7 tex: Tension = tex × 0.75g
4.5 Remove and discard the following nine lengths of yarn.
4.6 Repeat 4.4 and 4.5 four more times.
4.7 Repeat 4.4 to 4.6 on another part of the sample to give a total of 10 length measurements.
5. Calculation and results
5.1 calculate the mean stitch length in mm and % accuracy from the 10 length
measurements. for plain single jersey and interlock, stitch length(mm)=X/100.
For 1×1 rib, stitch length (mm) =X/200 Where X is the mean length of yarn unraveled 100 visible wales.
5.2 Repeat results correct to 2 decimal places.
N.B:For any construction other then those mentioned in 5.1 the procedure for removal of test length is modified so that at least one complete structural unit is assessed.
Calculation of results may also need to be revised.
Mass per Unit Area of Weft Knitted Fabric
1.Principle
The mass per unit area is determined by exposing a fabric sample to the standard by exposing a fabric sample to the standard for testing textile unit it has reached equilibrium with that atmosphere. Specimens of known dimensions are than taken and weight and the mass per unit area of the sample calculated.
2. Apparatus
2.1 Circular Cutter Of Nominal Area Of 100 Cm2 .
2.2 Analytical Balance.
2.3 Means For Providing The Standard Atmosphere For Testing Textiles Specified In
B.S.1051 and ISO 139.RH 65% ± 2% at 200C ± 20C.
3. Test samples
Test sample should be sufficiently large to enable to 5 specimens of 100 cm2 to be
taken, spaced to give a good representation of the sample, avoiding selvedge and/orcentre creases.
4.0 Test procedure
4.1 Condition the sample in the standard atmosphere for textiles (Ref. 2.3) until it has
reached equilibrium.
4.2 Using the circular of area 10 cm2 cut five test specimens (Ref. 3.0) .
4.3 Leave specimens to condition for one hour.
4.4 Measure the area of each test specimen and record measurements (this is necessary) because some knitted fabrics may be stretched during cutting.
4.5 Weigh each specimen to an accuracy of 0.0001g and record the weights.
5. 0 Calculation of Results
5.1 If one measuring the area of the test specimen it is found to be 100 cm2 calculated
Mass per unit area of the fabric using formula: Mua = m×100
Where, Mua is the mass per unit area in grammas per square meter of the
Fabric after conditioning in the standard atmosphere for testing, and
m is the mass in grams of the specimen.
If the area of the test specimen was less or greater than 100cm2 the calculation should be altered as follows:
Mua = (1000cm2 × m)/x
Where, x = actual area of the test specimen in cm2
5.2 Calculate the mean weight in g/m2 meter of the sample and % accuracy.
5.3 Report results correct to 1 decimal place.
Tightness Factor
Theory: Munden first suggested the use of a factor to indicate the relative tightness or looseness of plain weft knitted structure, to be used in a similar manner to that of the cover factor in the weaving industry. Originally termed the cover factor but now referred to as the tightness factor (TF), he defined if as the ratio of the area covered by the yarn in one loop to the occupied by that loop.
The total area covered by the yarn is; s×l×d,
Where, l=loop length in mm
d=yarn diameter in mm
Introducing the expression, S=kS /l, the area covering one 1cm of the fabric is,
KS× l× d KS×d
————— = ———
l ×100 100l
A correction for the four areas of each stitch is covered by two thickness of yarn is then necessary, together with an expression of yarn diameter in terms of linear density. When comparing the structure of the same type of yarn in similar state of relaxation, it is possible to use the simplified formula.
T.F =√Tex / l in S.I units (for cotton fabric)
Dimensional changes induced in 100% cotton weft knitted fabric during a selected washing procedure.
1.Principle: A fabric is subjected to a specified washing procedure, dried under the appropriate conditions and any changes in dimension determined.
2.0 Apparatus:
2.1 Means for providing the specified washing and drying condition.
2.2. The two Perspex templates:
a) 25×25cm
b) 50×50cm
Both the having three equidistantly located measuring marks on all sides.
2.3. Ruler and indelible pen.
2.4 Means for providing the standard atmosphere for testing textiles specified in B.s 1051 and ISO 139, RH 65%±2% at200c
3.Test samples:
Samples should be sufficiently large to enable 5 test specimens of single thickness to be prepared of 70×70cm or 6 test specimens of 45×45cm. They should be spaced to give a good representation of the sample avoiding selvedges and/or crease marks.
3.1 specimen preparation:
3.1.1. Condition the test sample in the standard atmosphere for testing textile (Ref.-2.4) until it has reached equilibrium.
3.1.2 Lay the sample on a flat horizontal surface, removing wrinkles without stretching.
3.1.3 prepare five test specimens of 70×70 cm or 6 specimens 45×45 cm from the sample ,spaced to give a good representation ,avoiding selvedges and/or crease marks. Case specimen should be minimum of 20cm larger in each direction than the required size of template,e.g.25×25cm template-specimen size 45×45 cm ; 50×50 cm template – specimen size 70×70 cm. where sample size permits, the
larger template should always be used.
3.1.4 Place the required size of template centrally on a specimen so that the edge follows a wale line.
3.1.5. Define the test area by drawing round the template, marking the position of the measuring marks .remove the template and clearly define the measuring marks on all side of the square.
3.1.6 measure and record the distance between the 3 pairs of measuring marks for width and the 3pairs of measuring marks for length.
3.1.7. repeat 3.1.4 -3.1.6 for the remaining 4 or 5 specimens in turn.
4.0. Test procedure
4.1. Prepare specimens as described in 3.0.
4.2 subject specimens to the specified washing and drying procedure.
4.3 After completion of the specified washing and drying procedure lay the specimens on a flat horizontal surface, removing wrinkles without stretching.
4.4. Condition the specimens in the standard atmosphere for testing textiles (Ref.2.4) until they have reached equilibrium.
4.5 Re measure and record the distances between the 3 pairs of measuring marks for width and the 3 pairs of measuring marks for length.
5.Calculation of results:
5.1. Calculation the average changes in dimensions in both length and width directions for each specimen and express the results as percentages of the original average length and width measurements. Calculate the mean percentage changes in length and width for the five or six specimens.
5.2 Indicate an extension by using the prefix ext.
5.3 Report the results correct to 1 decimal place and state the specified washing and drying procedure.
Results and discussion
Knitted fabric properties for 32/2 and 20/2 Ne are following:
Table -9.1: Wales per 3cm for 32/2 Ne
| Types ofstructure | Wales per 3cm | Average value | ||||||||||
| 1×1 Rib | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | |
| 1×1 SkeletonRib | 45 | 45 | 45 | 45 | 45 | 45 | 45 | 45 | 45 | 45 | 45 | |
| 2×2 SwissRib | 60 | 60 | 66 | 54 | 60 | 66 | 60 | 54 | 60 | 60 | ||
| 2×2 EnglishRib | 54 | 54 | 48 | 60 | 54 | 48 | 60 | 54 | 54 | 54 | 54 | |
| 6×3 DerbyRib | 69 | 69 | 63 | 66 | 63 | 66 | 66 | 6 | 66 | 66 | 66 | |
Table -9.2: Wales per 3cm for 20/2 Ne
| Types ofstructure | Wales per 3cm | Average value | ||||||||||
| 1×1 Rib | 48 | 42 | 42 | 45 | 45 | 48 | 45 | 45 | 45 | 45 | 45 | |
| 1×1 SkeletonRib | 42 | 42 | 45 | 42 | 39 | 42 | 42 | 42 | 42 | 42 | 42 | |
| 2×2 SwissRib | 54 | 54 | 54 | 54 | 54 | 54 | 54 | 54 | 54 | 54 | 54 | |
| 2×2 EnglishRib | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | |
| 6×3 DerbyRib | 63 | 63 | 63 | 63 | 60 | 63 | 66 | 66 | 63 | 60 | 63 | |
Table – 9.3: course per 3cm for 32/2Ne
| Types ofstructure | Course per 3cm | Average value | ||||||||||
| 1×1 Rib | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | |
| 1×1 SkeletonRib | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | |
| 2×2 SwissRib | 36 | 33 | 33 | 36 | 36 | 32 | 36 | 33 | 36 | 36 | 36 | |
| 2×2 EnglishRib | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | |
| 6×3 DerbyRib | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | |
Table – 9.4: course per 3cm for 20/2 Ne
| Types ofstructure | Course per 3cm | Average value | ||||||||||
| 1×1 Rib | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | |
| 1×1 SkeletonRib | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | |
| 2×2 SwissRib | 33 | 36 | 30 | 33 | 33 | 36 | 10 | 33 | 33 | 33 | 33 | |
| 2×2 EnglishRib | 33 | 10 | 33 | 36 | 33 | 33 | 36 | 33 | 30 | 33 | 33 | |
| 6×3 DerbyRib | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | |
Table – 9.5: Stitch density for 32/2 Ne
| Types ofstructure | Stitch density | Average value | ||||||||||
| 1×1 Rib | 176 | 176 | 176 | 176 | 176 | 176 | 176 | 176 | 176 | 176 | 176 | |
| 1×1 SkeletonRib | 165 | 165 | 165 | 165 | 165 | 165 | 165 | 165 | 165 | 165 | 165 | |
| 2×2 SwissRib | 240 | 240 | 264 | 216 | 240 | 264 | 240 | 240 | 216 | 240 | 240 | |
| 2×2 EnglishRib | 216 | 198 | 208 | 240 | 216 | 208 | 240 | 198 | 198 | 198 | 216 | |
| 6×3 DerbyRib | 253 | 253 | 231 | 242 | 231 | 242 | 242 | 253 | 242 | 242 | 242 | |
Table – 9.6: Stitch density for 20/2 Ne
| Types ofstructure | Stitch density(1×1) cm2 | Average value | ||||||||||
| 1×1 Rib | 160 | 140 | 140 | 150 | 150 | 160 | 150 | 150 | 150 | 150 | 150 | |
| 1×1 SkeletonRib | 140 | 140 | 150 | 140 | 130 | 140 | 140 | 140 | 140 | 140 | 140 | |
| 2×2 SwissRib | 198 | 180 | 198 | 216 | 198 | 198 | 216 | 198 | 180 | 198 | 198 | |
| 2×2 EnglishRib | 176 | 192 | 160 | 176 | 176 | 192 | 160 | 176 | 176 | 176 | 176 | |
| 6×3 DerbyRib | 210 | 210 | 210 | 210 | 200 | 210 | 220 | 220 | 210 | 200 | 210 | |
Table – 9.7: Stitch length for 32/2 Ne
| Types ofStructure | Stitch length(mm) | Avg. value | ||||||||||
| 1×1 Rib | 4.16 | 4.10 | 4.20 | 4.08 | 4.20 | 4.06 | 4.24 | 4.10 | 4.12 | 4.20 | 4.146 | |
| 1×1 SkeletonRib | 5.10 | 4.80 | 5.14 | 4.98 | 5.10 | 4.90 | 5.12 | 4.96 | 5.10 | 5.00 | 5.02 | |
| 2×2 SwissRib | 4.475 | 4.125 | 4.425 | 4.125 | 4.175 | 4.175 | 4.425 | 4.125 | 4.475 | 4.2 | 4.303 | |
| 2×2 EnglishRib | 4.8 | 5 | 4.875 | 5 | 4.825 | 5 | 4.85 | 5.125 | 4.825 | 5.05 | 4.94 | |
| 6×3 DerbyRib | 4.32 | 4.10 | 4.46 | 4.18 | 4.46 | 4.20 | 4.48 | 4.18 | 4.40 | 4.18 | 4.30 | |
Table – 9.8: Stitch length for 20/2 Ne
| Types of |
structure Stitch length Average
value1×1 Rib4.064.284.104.304.084.254.104.284.064.29
4.18
1×1 Skeleton
Rib4.604.754.604.804.654.774.624.754.604.70
4.69
2×2 Swiss
Rib4.624.444.624.434.634.454.624.444.614.44
4.53
2×2 English
Rib4.964.965.244.985.254.975.254.985.254.97
5.08
6×3 Derby
Rib4.204.454.184.464.214.444.204.454.214.44
4.324
Table – 9.9: Tightness factor for 32/2 Ne
| Types of |
structure Tightness factor Average
value1×1 Rib1.461.481.451.491.451.491.431.481.471.45
1.465
1×1 Skeleton
Rib1.191.271.181.221.191.241.191.221.191.22
1.211
2×2 Swiss
Rib1.361.471.371.471.361.461.371.471.361.46
1.412
2×2 English
Rib1.271.221.251.221.261.221.251.191.261.20
1.234
6×3 Derby
Rib1.411.481.361.451.361.451.351.451.381.45
1.414
Table – 9.10: Tightness factor for 20/2 Ne
| Types of |
structure Tightnes factor Average
value1×1 Rib1.891.801.871.791.881.811.871.801.891.791.8341×1 Skeleton
Rib1.191.271.181.221.191.241.191.221.191.221.2112×2 Swiss
Rib1.661.731.661.731.661.731.661.731.671.731.6962×2 English
Rib1.551.551.471.531.461.291.461.541.461.551.5136×3 Derby
Rib1.831.731.841.721.831.731.831.731.831.731.78
Table – 9.11: GSM(g/m2) for 32/2 Ne
| Types of |
structure
GSM(g/m2)
Average
value
1×1 Rib243.6246.1241.1239.5242.3
242.52
1×1 Skeleton
Rib191.2193.5191.4189.1192.2
191.48
2×2 Swiss
Rib337.52335337.1335.89337.6
336.62
2×2 English
Rib282283.1282281.6283
282.34
6×3 Derby
Rib324.1324.8325323324
324.18
Table – 9.12: GSM(g/m2) for 20/2 Ne
| Types of |
structure
GSM(g/m2)
Average
value
1×1 Rib423421.4422424.63424
423.01
1×1 Skeleton
Rib352354.6351.3351351.65
352.11
2×2 Swiss
Rib530532.1534530528.35
530.89
2×2 English
Rib502506.8504.4507.39506
505.32
6×3 Derby
Rib568.23561564.6568565
565.37
Table – 9.13: Dimensional Stability along Wale direction 20/2 Ne
| Types of |
structure Shrinkage% Average
value1×1 Rib1.921.922.22.31.92.02.12.22.1
2.062
1×1 Skeleton
Rib3.13.43.32.93.123.193.413.303.43.4
3.252
2×2 Swiss
Rib5.214.895.505.015.035.114.915.035.504.92
5.111
2×2 English
Rib6.797.077.237.127.457.2277.17.27.2
7.12
6×3 Derby
Rib99.29.69.329.329.068.939.329.318.93
9.199
Table – 9.14: Dimensional Stability along Course direction 20/2 Ne
| Types of |
structure Extension% Average
value1×1 Rib1.11.021.131.251.411.211.081.121.251.41
1.198
1×1 Skeleton
Rib2.412.892.472.673.113.03.042.702.892.67
2.785
2×2 Swiss
Rib3.13.33.333.013.323.013.323.103.013.12
3.162
2×2 English
Rib4.504.244.984.764.384.344.264.834.344.38
4.501
6×3 Derby
Rib8.18.647.907.987.978.047.788.048.47.78
8.063
Table – 9.15: Dimensional Stability along Wale direction 32/2 Ne
| Types of |
Structure Shrinkage% Average
value1×1 Rib2.32.671.922.21.891.92.02.12.22.12.581×1 Skeleton
Rib5.214.895.505.015.035.114.915.035.504.925.1112×2 Swiss
Rib6.797.077.237.127.457.2277.17.27.27.122×2 English
Rib8.799.078.239.128.458.2299.19.29.28.8386×3 Derby
Rib10.710.210.39.929.8210.610.610.110.910.310.344
Table – 9.16: Dimensional Stability along Course direction 32/2 Ne
| Types of |
Structure Extension% Average
value8.8381×1 Rib3.193.33.133.013.323.113.323.103.013.223.1621×1 Skeleton
Rib5.505.244.984.765.385.345.264.835.345.385.2012×2 Swiss
Rib8.18.647.907.987.978.047.788.048.47.788.0632×2 English
Rib8.799.078.239.128.458.2299.19.29.28.8386×3 Derby
Rib12.112.411.911.811.912.411.812.212.411.812.07
Table-19.17: Comparison of 1×1 Rib and 1×1 Skeleton Rib
| 1×1 Rib | 1×1 Skeleton Rib | |||
| /2 Ne | 20/2 Ne | 32/2 Ne | 20/2 Ne | |
√
√ Course per 3cm
=
=
=
=
Stitch density
√
√ Stitch length
√
√Tightness factor
√
√ GSM
√
√ Shrinkage%
√
√Extension%
√
√
Table 9.18: Comparison of 1×1 Rib and 2×2 Swiss Rib
| Properties | 1×1 Rib | 2×2 Swiss Rib | ||
| 32/2 Ne | 20/2 Ne | 32/2 Ne | 20/2 Ne | |
| Wales per 3cm | √ | √ | ||
| Course per 3 cm | = | = | = | = |
| Stitch density | √ | √ | ||
| Stitch length | √ | √ | ||
| Tightness factor | √ | √ | ||
| GSM | √ | √ | ||
| Shrinkage% | √ | √ | ||
| Extension% | √ | √ | ||
(√) indicates property value is higher and Blank indicate property value is lower .
(=) indicates property value is equal in both structures.
Table-9.19: Comparison of 1×1 Rib and 2×2 English Rib
Properties | 1×1 Rib | 2×2 English Rib | ||
30/2 Ne | 20/2 Ne | 32/2 Ne | 20/2 Ne | |
Wales per 3cm | √ | √ | ||
Course per 3cm | √ | √ | ||
Stitch density | √ | √ | ||
Stitch length | √ | √ | ||
Tightness factor | √ | √ | ||
GSM | √ | √ | ||
Shrinkage% | √ | √ | ||
Extension% | √ | √ | ||
Table-9.19: Comparison of 1×1 Rib and 6×3 Derby Rib
Properties | 1×1 Rib | 6×3 Derby Rib | ||
32/2 Ne | 20/2 Ne | 32/2 Ne | 20/2 Ne | |
Wales per 3cm | √ | √ | ||
Course per 3cm | = | = | = | = |
Stitch density | √ | √ | ||
Stitch length | √ | √ | ||
Tightness factor | √ | √ | √ | √ |
GSM | ||||
Shrinkage% | √ | √ | ||
Extension% | √ | √ | ||
(√) indicates property value is higher and Blank indicate property value is lower .
(=) indicates property value is equal in both structures.
Table-9.20: Comparison of 2×2 English Rib and 2×2 Swiss Rib
Properties | 2×2 English Rib | 2×2 Swiss Rib | ||
32/2 Ne | 20/2 Ne | 32/2 Ne | 20/2 Ne | |
Wales per 3cm | √ | √ | ||
Course per 3cm | = | = | = | = |
Stitch density | √ | √ | ||
Stitch length | √ | √ | ||
Tightness factor | √ | √ | ||
GSM | √ | √ | ||
Shrinkage% | √ | √ | ||
Extension% | √ | √ | ||
Table-9.21: Comparison of 2×2 English Rib and 1×1Skeleton Rib
Properties | 2×2 English Rib | 1×1 Skeleton Rib | ||
32/2 Ne | 20/2 Ne | 32/2 Ne | 20/2 Ne | |
Wales per 3cm | √ | √ | ||
Course per 3cm | √ | √ | ||
Stitch density | √ | √ | ||
Stitch length | √ | √ | ||
Tightness factor | √ | √ | ||
GSM | √ | √ | ||
Shrinkage% | √ | √ | ||
Extension% | √ | √ | ||
(√) indicates property value is higher and Blank indicate property value is lower .
(=) indicates property value is equal in both structures.
Table-9.22: Comparison of 2×2 English Rib and 6×3 Derby Rib
Properties | 2×2 English Rib | 6×3 Derby Rib | ||
32/2 Ne | 20/2 Ne | 32/2 Ne | 20/2 Ne | |
Wales per 3cm | √ | √ | ||
Course per 3cm | √ | √ | ||
Stitch density | √ | √ | ||
Stitch length | √ | √ | ||
Tightness factor | ||||
GSM | √ | √ | ||
Shrinkage% | √ | √ | ||
Extension% | √ | √ | ||
Table-9.23: Comparison of 2×2 English Rib and 6×3 Derby Rib
Properties | 2×2 Swiss Rib | 6×3 Derby Rib | ||
30/2 Ne | 20/2 Ne | 32/2 Ne | 20/2 Ne | |
Wales per 3cm | √ | √ | ||
Course per 3cm | √ | √ | ||
Stitch density | √ | √ | ||
Stitch length | √ | √ | ||
Tightness factor | √ | √ | ||
GSM | √ | √ | ||
Shrinkage% | √ | √ | ||
Extension% | √ | √ | ||
(√) indicates property value is higher and Blank indicate property value is lower.
(=) indicates property value is equal in both structures.
Conclusion
- We found that the values of the properties Wales per 3cm, Stitch density, Tightness factor, GSM are minimum in 1×1 Skeleton Rib.
- In 1×1 Rib we found that the values of the properties Wales per 3cm, Stitch density, Tightness factor, GSM are higher than the 1×1 Skeleton Rib.
- In 2×2 English Rib values of the properties wales per 3cm, Course per 3 cm, stitch length ,Stitch density, Stitch length, Tightness factor, Shrinkage%, extension% are higher than the 1×1 Rib.
- In 2×2 Swiss rib values of the of the properties wales per 3cm, Course per 3 cm, stitch length ,Stitch density, Stitch length, Tightness factor, Shrinkage%, extension% are higher than the 1×1 Rib..
- In 6×3 Derby rib values of the properties are higher than other structure.
- Shrinkage and Extension percentage increase with the increase of needle drop in knitting.